5.2 保存力と中心力
一般に力
![]() は位置ベクトル
は位置ベクトル
![]() だけでなく、速度
だけでなく、速度
![]() , 時間
, 時間 ![]() 等
の函数である:
等
の函数である:
![]() . 今、
. 今、
![]() が
が
![]() だけの函数
のとき、
だけの函数
のとき、
![]() を「力の場」という。
一般に、空間の各点
を「力の場」という。
一般に、空間の各点 ![]() にベクトルが与えられたとき、そのベクトルの
総体を「ベクトル場」という。同様に、空間の各点
にベクトルが与えられたとき、そのベクトルの
総体を「ベクトル場」という。同様に、空間の各点 ![]() にスカラー量が
与えられたとき、そのスカラーの総体を「スカラー場」という
にスカラー量が
与えられたとき、そのスカラーの総体を「スカラー場」という
以下、簡単のため
![]() を仮定する。
を仮定する。
仕事は一般には、運動の起点 ![]() と終点
と終点 ![]() 以外にその運動の経路
以外にその運動の経路 ![]() にも
依存するため、それを
にも
依存するため、それを
![]() と書く。
と書く。
(例)
2 次元の運動で、
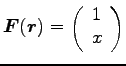 , かつ
, かつ ![]() が座標原点、
が座標原点、
![]() のとき、
のとき、
![]() から
から ![]() まで引いた直線の経路を
まで引いた直線の経路を
![]() ,
,
![]() を
を
![]() ,
,
![]() を
を
![]() とすると
とすると
![]() が
が ![]() ,
, ![]() にはよるが、経路
にはよるが、経路 ![]() には
よらないとき、
には
よらないとき、
![]() を「保存力」という。
この場合、ポテンシャル(位置エネルギー)による記述が可能である。
を「保存力」という。
この場合、ポテンシャル(位置エネルギー)による記述が可能である。
(力が保存力であるための条件)
線積分
![]() に対して、
経路を逆に辿った場合の線積分を
に対して、
経路を逆に辿った場合の線積分を
![]() =
=
![]() で表す。
で表す。
![]() である。
また別の経路
である。
また別の経路
![]() を考えると、
を考えると、
![]() のとき、
のとき、
![]() . つまり、
. つまり、
![]() .
すなわち、
.
すなわち、![]() から
から ![]() を巡って、再び
を巡って、再び ![]() に帰ってくる
閉じた経路を
に帰ってくる
閉じた経路を
![]() とすると
とすると
![]() .
これは、しばしば
.
これは、しばしば
![]() と書かれる。
すなわち、「
と書かれる。
すなわち、「
![]() が保存力なら、経路を一周するとその力が
した仕事はゼロ」である。
が保存力なら、経路を一周するとその力が
した仕事はゼロ」である。
また逆に、任意の閉じた経路に対して
![]() ならば、
ならば、
![]() は保存力である。実際、起点
は保存力である。実際、起点 ![]() , 終点
, 終点 ![]() を巡る 1 周の線積分を
考えると、任意の
を巡る 1 周の線積分を
考えると、任意の ![]() ,
,
![]() に対して
に対して
![]() . つまり
. つまり
![]() .
従って、
.
従って、
![]() は
は ![]() によらず
によらず ![]() である。
である。
まとめると
一般に
![]() が保存力なら、起点
が保存力なら、起点 ![]() を固定して
を固定して
(力とポテンシャルの関係)
以下、
![]() は保存力とする。
は保存力とする。
(gradient の幾何学的意味)
Taylor 展開より
(中心力)
万有引力の様に、ポテンシャルエネルギー
![]() が
が
![]() の
大きさ
の
大きさ
![]() だけの函数のとき、そこから導かれる保存力を
「中心力」という。このとき
だけの函数のとき、そこから導かれる保存力を
「中心力」という。このとき
参考
(偏微分、全微分) (2 変数で説明する)
2 変数の連続函数 ![]() に対して
に対して
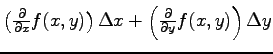 を 2 変数函数
を 2 変数函数
2 階の偏微分は
(微分形式)
一般に、2 次元平面内で連続な函数 ![]() ,
, ![]() に対して
に対して
(1 変数の場合)
![]() (連続) なら、
(連続) なら、
![]() を積分して
を積分して
(線積分)
(区分的に) 微分可能な経路
![]()
![]() with
with
![]() とすると
とすると
(微分形式の原始函数)
微分形式
![]() が連続的微分可能な函数
が連続的微分可能な函数 ![]() を
用いて
を
用いて
![]() と書ける時、
と書ける時、![]() を微分形式
を微分形式 ![]() の
原始函数という。この時
の
原始函数という。この時
(命題) 微分形式 ![]() が平面内で原始函数をもつ
が平面内で原始函数をもつ
![]() 平面内の任意の閉じた経路
平面内の任意の閉じた経路 ![]() に対して
に対して
![]()
(証明)
![]()
![]() ,
, ![]() として、O.K.
として、O.K.
![]()
![]() に対して、経路の取り方によらず
に対して、経路の取り方によらず
(H. カルタン「複素函数論」(岩波) 参照)