


運動の保存量
物理学基礎論 A
基本的例題(I)
第 7 講 (平成 19 年 5 月 22 日)
(基本的例題-続き-)
2. 斜面上の運動
斜面に沿って下方向に 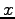 -軸、斜面に垂直方向に
-軸、斜面に垂直方向に 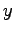 -軸をとる。
斜面の傾きを
-軸をとる。
斜面の傾きを 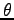 とする。
摩擦のない場合は、斜面に垂直な方向の力は釣合う。つまり
とする。
摩擦のない場合は、斜面に垂直な方向の力は釣合う。つまり
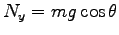 . 斜面に平行な力は
. 斜面に平行な力は
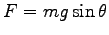 .
そこで運動方程式は
.
そこで運動方程式は
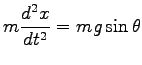 |
|
|
(0) |
つまり、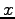 -軸方向に加速度
-軸方向に加速度
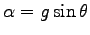 の定加速運動をする:
の定加速運動をする:
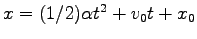 . ここに、
. ここに、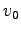 ,
, 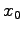 はそれぞれ
はそれぞれ
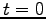 における速度と位置である。
における速度と位置である。
(摩擦のある場合)
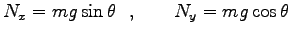 |
|
|
(0) |
と力が釣合っており、初め静止しておれば静止を続ける。斜面の傾き 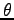 を徐々に大きくしていった時、
を徐々に大きくしていった時、
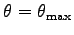 で動き出す
とすると、
で動き出す
とすると、
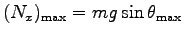 .
.
一般に接線方向の抗力(摩擦力) 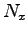 は垂直抗力
は垂直抗力 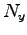 に比例する。
上の場合は
に比例する。
上の場合は
 である。
である。
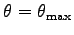 の時
の
の時
の
 を最大摩擦係数という。
を最大摩擦係数という。
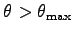 とすると、物体は滑り始める。
この時の摩擦力(滑り摩擦力) も垂直抗力
とすると、物体は滑り始める。
この時の摩擦力(滑り摩擦力) も垂直抗力 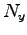 に比例する。
に比例する。
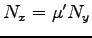 (一般に
(一般に
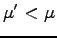 )
)
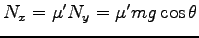 より
より 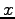 -軸方向の力は
-軸方向の力は
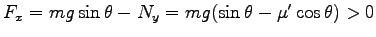 .
そこで、運動方程式は
.
そこで、運動方程式は
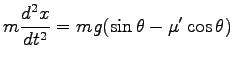 |
|
|
(0) |
つまり、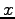 -軸方向に加速度
-軸方向に加速度
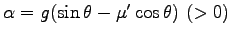 の定加速運動をする。
最大静止摩擦係数や滑り摩擦係数 (動摩擦係数ともいう) は物体の質量
によらず、斜面と物体が触れあう面の性質だけで決まる。
の定加速運動をする。
最大静止摩擦係数や滑り摩擦係数 (動摩擦係数ともいう) は物体の質量
によらず、斜面と物体が触れあう面の性質だけで決まる。
3. 等速円運動
伸び縮みしない糸で結ばれた、平面上の半径 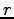 の円運動を考える。
2 次元極座標で考えるのが便利である。極座標での加速度の公式、
の円運動を考える。
2 次元極座標で考えるのが便利である。極座標での加速度の公式、
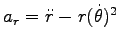 ,
,
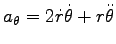 を用いて、運動方程式は
を用いて、運動方程式は
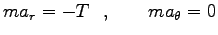 |
|
|
(0) |
である。ここに、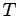 は糸の張力である。
は糸の張力である。
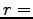 一定、より
一定、より 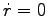 ,
,
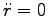 から 角速度
から 角速度
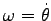 を
使うと
を
使うと
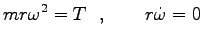 |
|
|
(0) |
二番目の式から 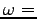 一定、従って
一定、従って
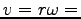 一定。
また、
一定。
また、
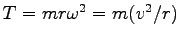 . つまり、糸の張力
. つまり、糸の張力 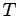 は速度
は速度 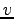 の
2 乗に比例する。
の
2 乗に比例する。
(宿題) 静止衛星
地球赤道上を地球の自転と同じ周期でまわる人工衛星。
高度 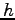 をいくらにすればよいか?
(答: 約 3 万 6 千 km)
をいくらにすればよいか?
(答: 約 3 万 6 千 km)
4. 単振動
壁に取り付けたバネによる物体の振動。働く力は横方向に
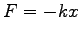 (
(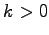 : バネ定数) これは、力が位置だけの函数の
例である。運動方程式は
: バネ定数) これは、力が位置だけの函数の
例である。運動方程式は
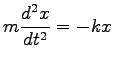 |
|
|
(0) |
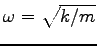 とおくと
とおくと
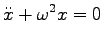 |
|
|
(0) |
一般解は 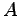 ,
, 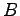 を時間に依存しない定数として
を時間に依存しない定数として
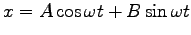 と表される。
と表される。
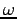 は角速度と同じ単位をもち、実際、下に見る様に等速円運動の
角速度と同じ意味を与えることが出来る。Eq. (5.6) は
線型 2 階微分方程式の簡単な例となっている。特に、
は角速度と同じ単位をもち、実際、下に見る様に等速円運動の
角速度と同じ意味を与えることが出来る。Eq. (5.6) は
線型 2 階微分方程式の簡単な例となっている。特に、
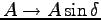 ,
,
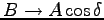 とすると、三角函数の
加法定理より、
とすると、三角函数の
加法定理より、
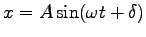 。
ここに
。
ここに 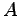 を振動の振幅、
を振動の振幅、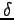 を初期位相 (
を初期位相 (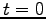 の
時の位相) という。三角函数の位相
の
時の位相) という。三角函数の位相
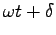 が
が 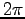 だけ
増えれば、変位
だけ
増えれば、変位 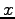 はもとの値にもどる。その意味で
はもとの値にもどる。その意味で
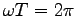 と
なる時間
と
なる時間 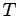 を周期と呼べば
を周期と呼べば
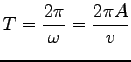 |
|
|
(0) |
(
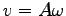 ) で
) で 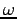 は等速円運動の角速度としての意味を持つ。
すなわち、単振動は円運動をある軸のまわりに射影したものである。
は等速円運動の角速度としての意味を持つ。
すなわち、単振動は円運動をある軸のまわりに射影したものである。
ここから、数学
(Euler の公式)
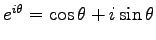
実際
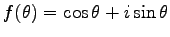 として、
として、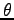 で
微分すると
で
微分すると
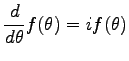 |
|
|
(0) |
この微分方程式は、以前の空気の抵抗がある時の放物運動のところで
試みたのと同様にして解ける。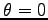 で
で 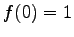 で
あることに注意すると、
で
あることに注意すると、
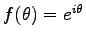 .
.
(複素数の極座標表示)
横軸に 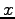 , 縦軸に
, 縦軸に 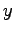 の代りに
の代りに 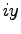 をとると
をとると
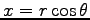 ,
,
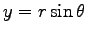 より
より
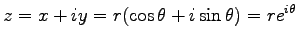 |
|
|
(0) |
と書ける。従って、
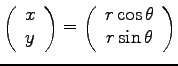 の 2 次元ベクトルは、
唯一の複素数
の 2 次元ベクトルは、
唯一の複素数
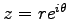 で表される。
これを「複素数の極座標表示」という。
で表される。
これを「複素数の極座標表示」という。
(Eq. (5.7) の一般解)
 ,
, 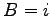 として
として
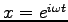 .
.
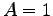 ,
, 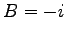 として (或は、左の複素共役をとって)、
として (或は、左の複素共役をとって)、
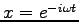 . 従って、Eq. (5.7) の一般解は
. 従って、Eq. (5.7) の一般解は
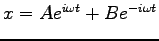 とも表わされる。
とも表わされる。
(複素数の指数函数) 通常の指数法則が成り立つ。つまり
| |
|
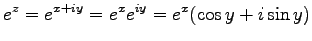 |
|
| |
|
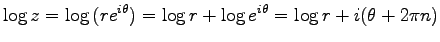 |
(0) |
ここに
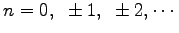 .
.
(Taylor 展開)
一般に函数 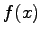 が
が
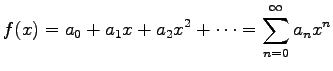 |
|
|
(0) |
と巾(ベキ)級数に展開できるとすると
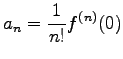 |
|
|
(0) |
が成り立つ。ここに、
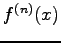 は
は 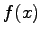 の
の 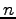 階の微分
を表す。これを、Taylor 展開という。
実は、
階の微分
を表す。これを、Taylor 展開という。
実は、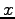 を
を
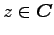 (複素数) としても成り立つ。すなわち
(複素数) としても成り立つ。すなわち
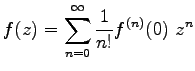 |
|
|
(0) |
複素函数 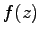 がこの様に巾級数に展開出来るとき、
がこの様に巾級数に展開出来るとき、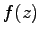 を
解析函数という。指数函数
を
解析函数という。指数函数 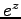 や sine, cosine 函数、
や sine, cosine 函数、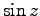 ,
,
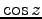 等の、いわゆる初等函数は全て解析函数である。
特に、
等の、いわゆる初等函数は全て解析函数である。
特に、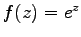 の時、
の時、
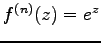 であるから
であるから
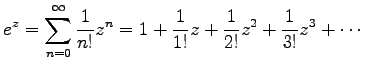 |
|
|
(0) |
は指数函数の巾級数展開であり、指数函数の定義を与えている。
更に、
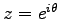 とおいて、実部と虚部ごと (
とおいて、実部と虚部ごと ( =実数とする) に
まとめると、Euler の公式により
=実数とする) に
まとめると、Euler の公式により
が得られる。これらは、sine, cosine 函数の巾級数展開である。
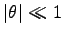 の時、特に有用である。
の時、特に有用である。
5. 単振子
伸び縮みしない長さ 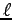 の糸に質量
の糸に質量 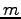 の重りをつけて吊す。
の重りをつけて吊す。
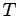 を糸の張力として、運動方程式は
を糸の張力として、運動方程式は
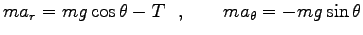 |
|
|
(0) |
である。ここに、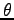 は糸の垂直方向からの振れ角である。
極座標表示で
は糸の垂直方向からの振れ角である。
極座標表示で 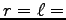 一定、より、
一定、より、
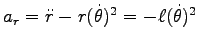 ,
,
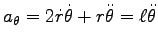 .
そこで
.
そこで
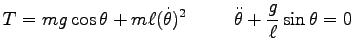 |
|
|
(0) |
が得られる。今度は
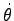 は一定ではない。
しかし、
は一定ではない。
しかし、
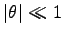 (振れ角は小さい) として
(振れ角は小さい) として
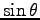 を
を 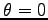 のまわりに展開して、
のまわりに展開して、
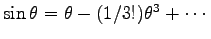 の
の 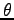 の1次
までとると、新しく
の1次
までとると、新しく
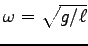 として
(
として
(
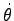 ではない!)、Eq. (5.18) の二番目の式は
ではない!)、Eq. (5.18) の二番目の式は
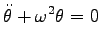 |
|
|
(0) |
となる。これは、単振動の式 Eq. (5.7) で
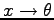 とした
ものだから
とした
ものだから
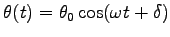 |
|
|
(0) |
ここに、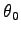 ,
, 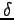 は任意定数である。
振動の周期は
は任意定数である。
振動の周期は
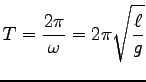 |
|
|
(0) |
(同じ 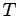 だが、張力の
だが、張力の 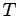 と区別する。)
すなわち、振動が小さい (
と区別する。)
すなわち、振動が小さい (
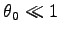 radian) 時は周期は
振幅
radian) 時は周期は
振幅 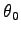 によらない。これを、「振り子の等時性」という。
また、
によらない。これを、「振り子の等時性」という。
また、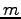 にもよらない。(ガリレオの観察)
にもよらない。(ガリレオの観察)



運動の保存量
物理学基礎論 A
基本的例題(I)
Yoshikazu Fujiwara
平成19年5月23日
![]() -軸、斜面に垂直方向に
-軸、斜面に垂直方向に ![]() -軸をとる。
斜面の傾きを
-軸をとる。
斜面の傾きを ![]() とする。
摩擦のない場合は、斜面に垂直な方向の力は釣合う。つまり
とする。
摩擦のない場合は、斜面に垂直な方向の力は釣合う。つまり
![]() . 斜面に平行な力は
. 斜面に平行な力は
![]() .
そこで運動方程式は
.
そこで運動方程式は
![]() は垂直抗力
は垂直抗力 ![]() に比例する。
上の場合は
に比例する。
上の場合は
![]() である。
である。
![]() の時
の
の時
の
![]() を最大摩擦係数という。
を最大摩擦係数という。
![]() とすると、物体は滑り始める。
この時の摩擦力(滑り摩擦力) も垂直抗力
とすると、物体は滑り始める。
この時の摩擦力(滑り摩擦力) も垂直抗力 ![]() に比例する。
に比例する。
![]() (一般に
(一般に
![]() )
)
![]() より
より ![]() -軸方向の力は
-軸方向の力は
![]() .
そこで、運動方程式は
.
そこで、運動方程式は
![]() の円運動を考える。
2 次元極座標で考えるのが便利である。極座標での加速度の公式、
の円運動を考える。
2 次元極座標で考えるのが便利である。極座標での加速度の公式、
![]() ,
,
![]() を用いて、運動方程式は
を用いて、運動方程式は
![]() をいくらにすればよいか?
(答: 約 3 万 6 千 km)
をいくらにすればよいか?
(答: 約 3 万 6 千 km)
![]() (
(![]() : バネ定数) これは、力が位置だけの函数の
例である。運動方程式は
: バネ定数) これは、力が位置だけの函数の
例である。運動方程式は
![]()
![]() として、
として、![]() で
微分すると
で
微分すると
![]() , 縦軸に
, 縦軸に ![]() の代りに
の代りに ![]() をとると
をとると
![]() ,
,
![]() より
より
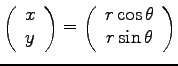 の 2 次元ベクトルは、
唯一の複素数
の 2 次元ベクトルは、
唯一の複素数
![]() ,
, ![]() として
として
![]() .
.
![]() ,
, ![]() として (或は、左の複素共役をとって)、
として (或は、左の複素共役をとって)、
![]() . 従って、Eq. (5.7) の一般解は
. 従って、Eq. (5.7) の一般解は
![]() とも表わされる。
とも表わされる。
![]() が
が
![]() の糸に質量
の糸に質量 ![]() の重りをつけて吊す。
の重りをつけて吊す。
![]() を糸の張力として、運動方程式は
を糸の張力として、運動方程式は