


>保存力と中心力
物理学基礎論 A
基本的例題(II)
運動の保存量 (時間に依存しない量) の主なものは
エネルギー、運動量、角運動量であり、これらはある条件のもとに
それぞれ次の保存則を満す。
- エネルギーの保存則
 スカラー量の保存 (内積に関係)
スカラー量の保存 (内積に関係)
- 運動量の保存則
 ベクトル量の保存
ベクトル量の保存
- 角運動量の保存
 ベクトル量の保存 (外積に関係)
ベクトル量の保存 (外積に関係)
これらは、いずれももとの運動方程式を積分して得られる。それ故、
これらの保存則を「運動方程式の積分形」という。
(保存則の効用)
- 運動の詳細によらない運動学 (kinematics) である。力の
性質 (保存力かどうか等) だけで決まる。
- エネルギー保存則はスカラー量の保存 (加算的:質点系で特に有用)
であり、しばしば運動方程式を直接解くより運動の解法が容易になる。
- 微視の世界では、力自身よりむしろポテンシャルの概念が
より本質的。

簡単のため、まず 1 質点の保存則を議論する。
5.1 仕事と運動エネルギー
1 質点の運動方程式
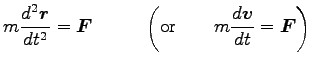 |
|
|
(0) |
と速度
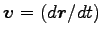 の内積をとる。
の内積をとる。
 |
|
|
(0) |
両辺を時刻 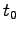 から
から 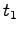 まで積分して
まで積分して
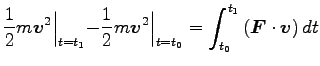 |
|
|
(0) |
ここに
| |
|
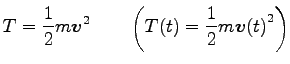 |
|
| |
|
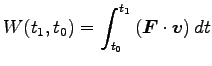 |
(0) |
を、それぞれ運動エネルギー (kinetic energy)、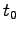 から
から 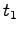 の
間に力
の
間に力
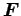 が質点にした仕事という。これらを使うと Eq. (5.3) は
が質点にした仕事という。これらを使うと Eq. (5.3) は
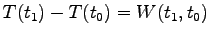 |
|
|
(0) |
と表わされる。すなわち、”質点の運動エネルギーの増分は
その質点になされた仕事に等しい。''
ここから、仕事とエネルギーは実は同じものである事がわかる。また、
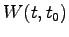 を
を 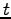 で微分して
で微分して
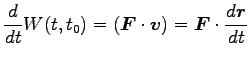 |
|
|
(0) |
これを仕事率という。
(仕事の意味)
質点の運動を、ある起点  からの距離
からの距離  を媒介変数として表わすと
を媒介変数として表わすと
| |
|
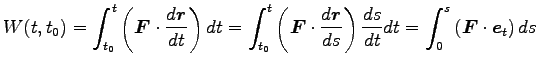 |
|
| |
|
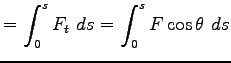 |
(0) |
ここに、
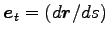 は第 3 章で議論した接線ベクトル、
は第 3 章で議論した接線ベクトル、
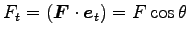 は力の接線成分、
は力の接線成分、
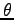 は各点における力と接線の間の角である。
は各点における力と接線の間の角である。
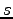 の積分で、区間
の積分で、区間 ![$ [0,s]$](img23.png) を
を 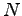 等分して
等分して
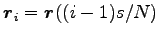 (
(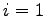 -
- 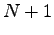 ),
),
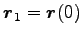 ,
,
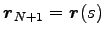 とすると
とすると
と書いて、これを経路 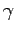 :
:
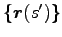
![$ s^\prime\in [0, s]$](img35.png) にそった線積分という。”仕事は一般には経路による。”
つまり、起点
にそった線積分という。”仕事は一般には経路による。”
つまり、起点
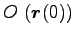 から終点
から終点
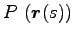 までのまた別の経路
を
までのまた別の経路
を
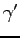 とすると、一般には
とすると、一般には
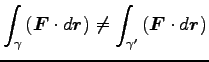 |
|
|
(0) |
実際、起点と終点を入れ替えるだけでも、仕事の符号は変る。
 と同じ経路を、今度は
と同じ経路を、今度は  を起点、
を起点、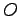 を終点と
する経路を
を終点と
する経路を 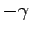 で表すと
で表すと
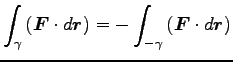 |
|
|
(0) |
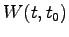 が経路によらない時、力が「保存力」であるという。
この時、
が経路によらない時、力が「保存力」であるという。
この時、
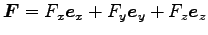 はあるスカラー
函数
はあるスカラー
函数
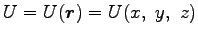 の偏微分係数(導関数) で書ける
(
の偏微分係数(導関数) で書ける
(
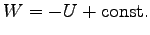 )。
)。
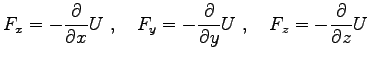 |
|
|
(0) |
これを、まとめて (ベクトル記法で)
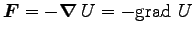 |
|
|
(0) |
と書き、
 をナブラ (nabla)、あるいは
をナブラ (nabla)、あるいは
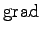 を
gradient いう。これらは、線型微分作用素 (operator) である。
を
gradient いう。これらは、線型微分作用素 (operator) である。
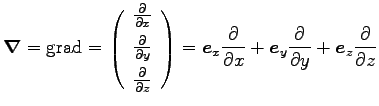 |
|
|
(0) |
(例)
重力、バネの力、万有引力、クーロン力、 保存力
保存力
摩擦、空気の抵抗、 非保存力
非保存力
[仕事とエネルギーの単位]
力 距離 =
距離 =
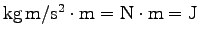 (ジュール)
(ジュール)  MKS 単位
MKS 単位
cgs 単位では
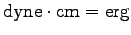 (エルグ)
(エルグ)
1 N=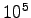 dyne より、 1 J=
dyne より、 1 J=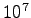 erg
erg
また、仕事率の単位は 1 W (ワット) = 1
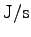
(簡単な例)
- 1 kg の重りを静かに 1 m 持ち上げるために
必要な仕事 (エネルギー) は約 9.8 N
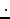 m=9.8 J
m=9.8 J
- 等速円運動では力の向きと速度の向きが垂直より、
力は仕事をしていない。
 運動エネルギーが保存される。
すなわち、速さ (速度の大きさ) が一定
運動エネルギーが保存される。
すなわち、速さ (速度の大きさ) が一定
- 1 次元運動
- (自由落下運動)
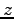 -軸を垂直上方向にとって、
重力は
-軸を垂直上方向にとって、
重力は
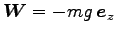 より
より
そこで、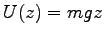 を重力の位置 (ポテンシャル) エネルギーとすると
を重力の位置 (ポテンシャル) エネルギーとすると
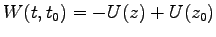 . そこで、
. そこで、
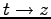 で書いて
Eq. (5.5) は
で書いて
Eq. (5.5) は
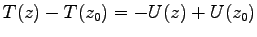 . つまり
. つまり
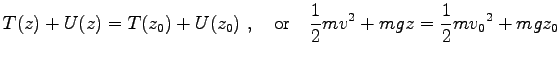 |
|
|
(0) |
これを、(力学的) エネルギーの保存則という。
- (バネの運動) 復元力は
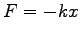 より
より
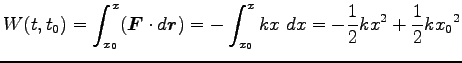 |
|
|
(0) |
そこで、
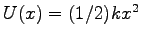 をバネの位置エネルギーとして
をバネの位置エネルギーとして
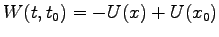 より
より
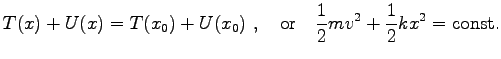 |
|
|
(0) |
- 万有引力ポテンシャル: 3 次元 (or 2 次元) 極座標で
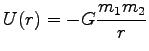 |
|
|
(0) |
偏微分の公式
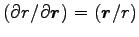 と動径方向の単位ベクトル
と動径方向の単位ベクトル
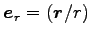 を用いると
を用いると
すなわち、万有引力は動径方向(の逆) を向く。
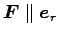 この様に力の方向が座標原点方向を向く力を「中心力」という。この時、
ポテンシャルは
この様に力の方向が座標原点方向を向く力を「中心力」という。この時、
ポテンシャルは
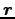 の向きによらず、その絶対値
の向きによらず、その絶対値
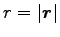 だけの
函数である。
だけの
函数である。



>保存力と中心力
物理学基礎論 A
基本的例題(II)
Yoshikazu Fujiwara
平成19年5月29日
![]() からの距離
からの距離 ![]() を媒介変数として表わすと
を媒介変数として表わすと
![]() が経路によらない時、力が「保存力」であるという。
この時、
が経路によらない時、力が「保存力」であるという。
この時、
![]() はあるスカラー
函数
はあるスカラー
函数
![]() の偏微分係数(導関数) で書ける
(
の偏微分係数(導関数) で書ける
(
![]() )。
)。
![]() 保存力
保存力
![]() 非保存力
非保存力
![]() 距離 =
距離 =
![]() (ジュール)
(ジュール) ![]() MKS 単位
MKS 単位
![]() (エルグ)
(エルグ)
![]() dyne より、 1 J=
dyne より、 1 J=![]() erg
erg
![]()