CSSデザインサンプル

はじめに

私が高校一年生のAIちゃんを知るようになったのは、私の妻が英語の家庭教師を始めたのがきっかけでした。私の妻は、東京都の中学校の臨時職員として英語を教えていたので、 AIちゃんの高校受験の為に英語の家庭教師を頼まれたのです。ところが、数学や理科も分からないと言われて、物理が専門の私の方に鉢が回ってきたのです。ところが、実際に会ってみると、高一の初めから学んだルート2の計算や２乗の二項定理などはほぼ完璧に出来るのに、簡単な分数の約分や通分が出来ない。非常にアンバランスな状況に気がつきました。四則演算は「読み書きそろばん」と言って、江戸時代から最も基本的な初等教育だったのに、それが何故かないがしろにされて、中学や高等学校で復習をしないまま、どんどん難しい数学に進んでいっていると言う現実に遭遇しました。そこで、数学(解析学)で一番基礎となる数とは何かとか、計算のルールをもう一度学び直すと、随分と多くの数学嫌いを治すことができるのではないかと思いました。それがこの学びを始めた理由です。ここでは、高校生を対象にもう一度数とは何かとか、計算のルールとは何かという最も基本的な勉強を振り返ってみたいと思います。

自然数、整数、足し算、引き算

数(かず)というと日常生活では普通 1, 2, 3, ...を指すが、数学ではこれを自然数 (英語では natural numbers) という。数という概念は、個数と順序数を抽象化したものとして人類の文明の早い段階から存在する。英語では、個数は one, two, three, ... と数え、順序は first, second, third, ... と数える。1, 2, 3, ...という表し方はアラビア数字と言われるが、それはインドで発明されたものがアラビア世界を通じてヨーロッパに伝わり、更に日本に輸入されたものである。中国では漢字の一, 二, 三, ... が使われる。また、時計の文字盤や書物の I章, II章, ... には、ローマ数字、I, II, III, ... なども使われる。いずれにせよ、人類が数という概念を得たことで高度な文明を発達させたことは間違いがない。

足し算は自然数の中で自由にできる。例えばみかんを1つ持っている人が更にみかん2つもらったとすると、みかんの数は全部で 1+2=3 つとなる。しかし、足し算の逆演算の引き算となると自然数だけでは自由に出来ない。例えば、みかん3つ持っている人がひとつ食べたとすると残りは 3-1=2 個である。二つ食べたとすると残りは 3-2=1 個。しかし、ひとつしかみかんを持っていない人がみかんを三つ食べようとしても、それは出来ない。ニつ不足する。これを \(1-3=-2\) と書いて、みかんが \(-2\) 個残ったと言うことも出来る。

もう一つの例は、無限に長いモノサシを考えて真ん中に 0 を取り右側に 1 cm ごとに 1, 2, 3, ... ととり、左側に同じく1 cm ごとに \(-1, -2, -3, ...\) ととる。(図1 参照) このような数字の格子点を考えた上で足し算、引き算を考える。例えば、1 を基準として右側に 2 つ進むことを \(1+2\) と考えると 3 が到達点である。(図2 参照) 同じように、引き算は左側に進むことに対応している。例えば、\(1-3=-2\) は 1 から出発して 3 だけ左に進んだ \(-2\) を表す。これを \(1+(-3)\) と考えると \(-3\) だけ右に進んだことに対応している。(図3 参照)

一般に、自然数 \(n=1,2, ...\) に負符号をつけたものを \(-n\) で表し、それを \(n\) の反数という。 \(-n\) の反数は \(-(-n)=n\) だから \(n\) である。ある数とその反数と加えると、\(n+(-n)=n-n=0\) だから零 (0) は足し算、引き算の中で特別の意味を持っている。自然数とその反数に 0 をつけ加えたもの全体を整数（英語では integers）という。(図1 参照) 数という概念を自然数から整数までに広げると、足し算、引き算が自由にできる。これを、整数は足し算、引き算に対して閉じているという。自然数は正の整数であり、引き算は負の整数を考えることにより、全て足し算に帰着できる。

高校 1 年も後期になれば集合とその記号を習うので、それらを積極的に使用すると自然数は \(\boldsymbol{N}=\left\{1, 2, 3, ...\right\}\) と表す。 (集合はアルファベットの大文字で表すので Natural numbers の \(N\) だが、特別の意味を持つので太文字を用いる。また、高校数学では有限集合しか扱わないが、ここでは簡単な無限集合も扱うことにする。) 集合の個々の要素 (あるいは、元) の自然数は、一般に \(n, m, ... \) 等で表す。すなわち \(n ∈ \boldsymbol{N}\) である。整数は、\(\boldsymbol{I}\) ではなしに \( \boldsymbol{Z}=\left\{-n, 0, n | n ∈ \boldsymbol{N}\right\}\) で表す。整数が足し算、引き算に対して閉じていることは、初等的な論理記号 ∈, ∀, ∃ 等を用いて

\[ n+m ∈ \boldsymbol{Z} \ \hbox{and}\ n-m ∈ \boldsymbol{Z} \quad \hbox{for} \ \forall n, m ∈ \boldsymbol{Z} \]

と表すことが出来る。

図1: 数直線 (後述)と整数点

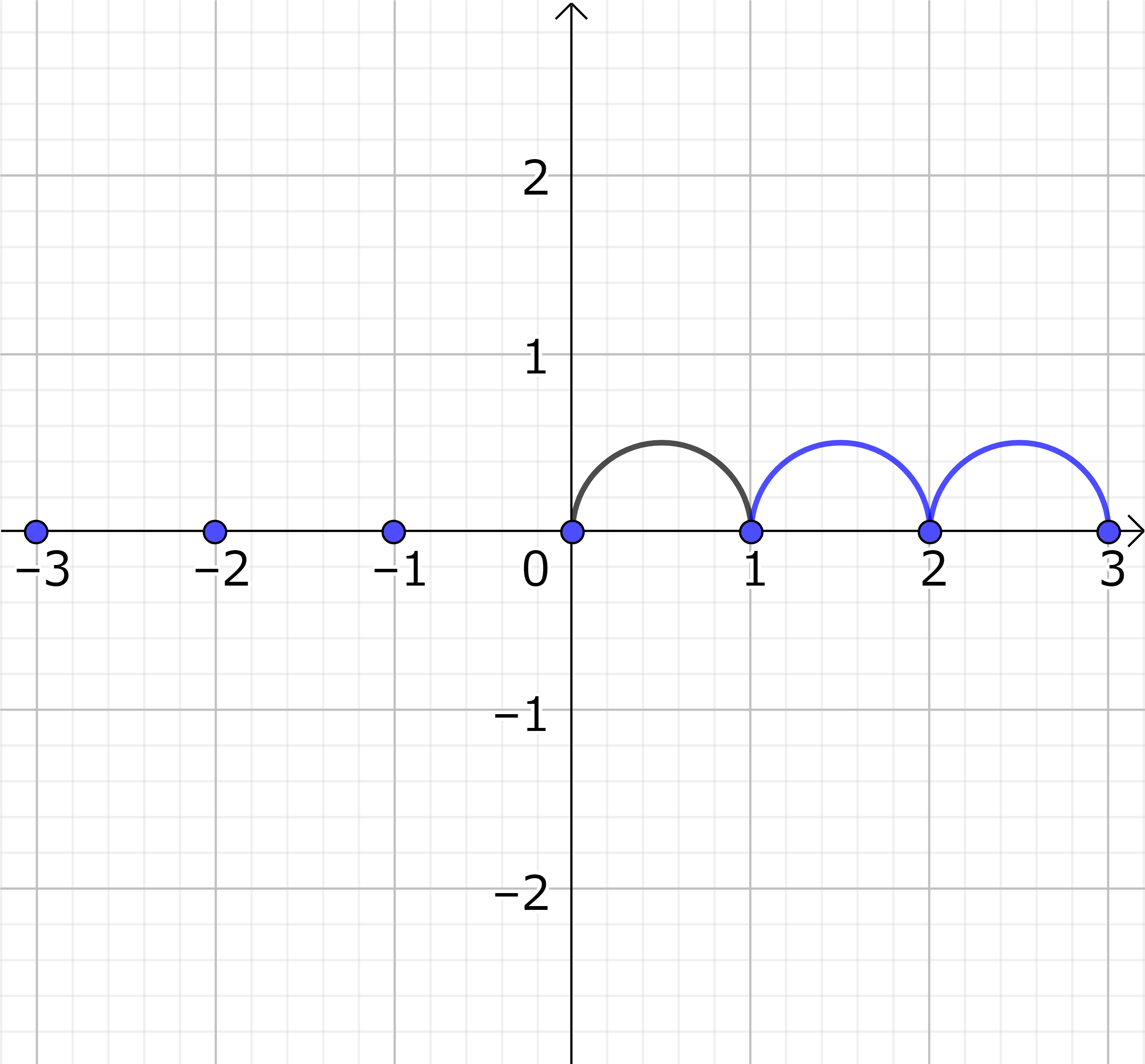
図2: \(1+2=3\)

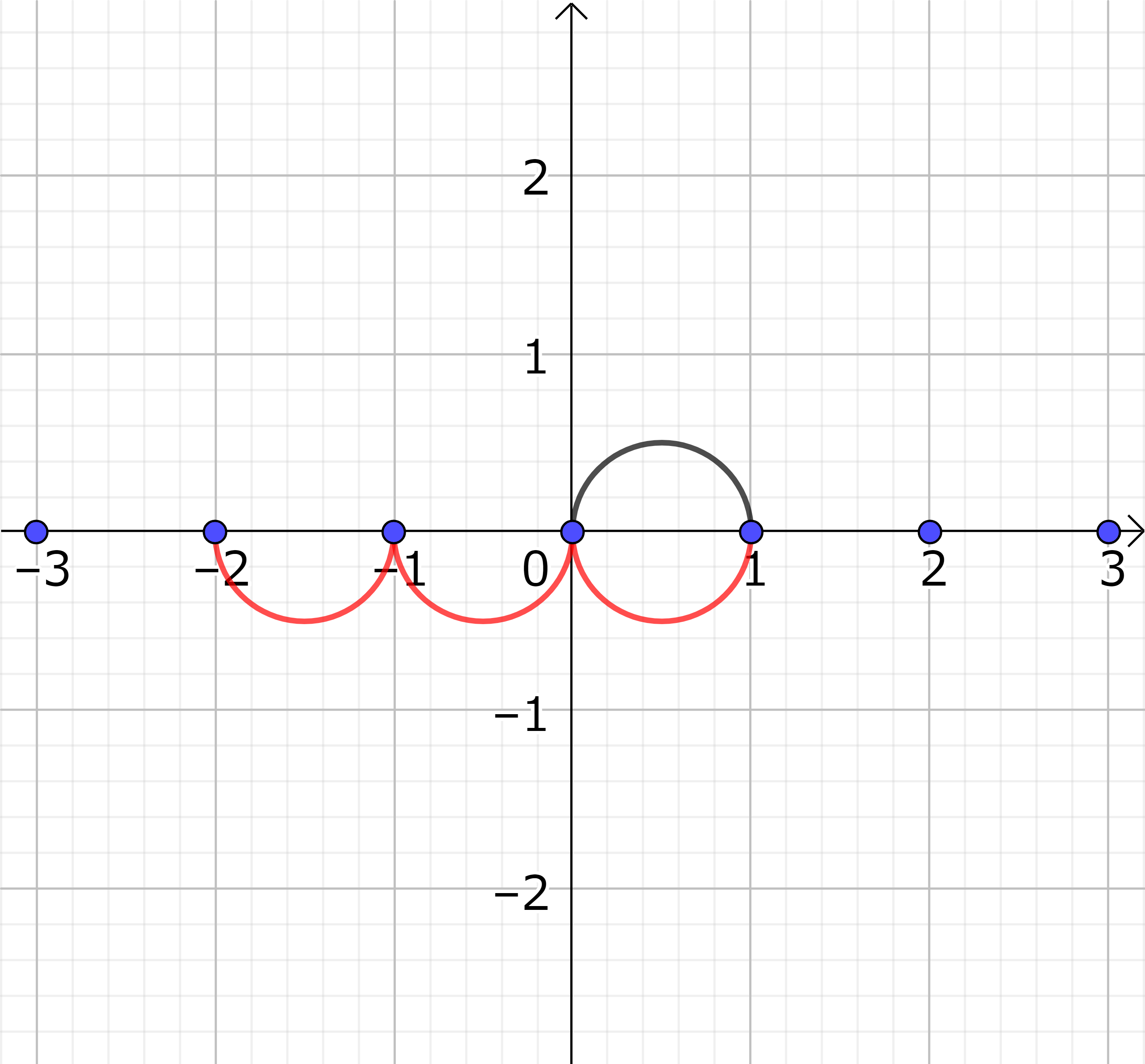
図3: \(1-3=1+(-3)=-2 \)

図4: \(2+2+2=2×3=6\)

掛け算、割り算、分数、有理数

掛け算、割り算にも足し算、引き算と同じような事情が存在する。例えばみかん2つ持っている人が3人いると、みかんは全部で2×3=6個ある。掛け算の意味は足し算を繰り返すことで、今の場合2を3回足して2+2+2=2×3=6 である。(図4 参照) このように自然数の中では掛け算は自由にできる。ところが、割り算はそういうわけにはいかない。6個のみかんを3人で割ると、一人あたり6÷3=2個となる。しかし、2個のみかんを3人で割ることはできない。そこで分数や小数の助けを借りることとなる。今の場合 \(2÷3=\frac{2}{3}\) あるいは 2/3となる。分数は一般に「分数=整数/整数」で定義される。(ここでは、印刷時の見栄えを良くするために、分数を横棒でなく出来るだけ斜線 / を使うことにする。) \(n\) を整数とするとき \(1/n\) を \(n\) の逆数と言う。分数に対してもその分子と分母をひっくり返したものを、もとの分数の逆数という。したがって、\(1/n\) の逆数は \(n\) である。ある数とその逆数をかけると必ず1となる。その意味で掛け算、割り算における1は足し算、引き算における0に対応している。数の概念を分数までに広げると、0で割ることをのぞいて、掛け算、割り算が自由にできる。整数と分数と合わせて有理数 (Rational numbers と言い、集合記号で \(\boldsymbol{Q}=\left\{\frac{p}{q} | p, q ∈ \boldsymbol{Z} \ \hbox{with} \ q \neq 0\right\}\) と表わす。 (\( \boldsymbol{R}\) は実数を表わすために取っておく。）分数 \(\frac{p}{q}=p/q\) は、母が子を背おっている様に見えるので、\(q\) を分母、\(p\) を分子という。

掛け算は常に足し算に帰着できるわけではない。例えば、2×1.5、あるいは 2×(3/2) は 2を1.5回あるいは、3/2回かけるとしたのでは意味をなさない。そこで、掛け算、割り算は足し算、引き算とは違うまた別の演算と考えたほうが良い。これらを合わせて四則(演算、あるいは計算)という。九九は掛け算を学ぶための出発点である。

四則演算には厳密なルールがある。\(a, b, c\) をこれから学ぶ任意の数や式として

\[a+b=b+a\,\quad a×b=b×a\quad (\hbox{交換法則}）\\ (a+b)+c=a+(b+c)\ ,\quad \\ (a×b)×c=a×(b×c)\quad (\hbox{結合法則}）\\ a×(b+c)=a×b+a×c\ , \quad \\ (a+b)×c=a×c+b×c\quad (\hbox{分配法則}）\]

が厳密に成り立つ。更に、計算の順序として掛け算、割り算は足し算、引き算よりも必ず先に行う。また、括弧（...) がある場合は括弧の中を先に計算し、いくつかの括弧が入れ子になっている場合には、一番内側の括弧の中から計算する。分数の分母、分子はそれぞれ括弧に囲まれているものと考える。

自然数の割り算、商と余り、偶数、奇数

自然数の割り算で答えがまた自然数になる時、元の数は割る数で割りきれるという。例えば 7÷2 は割切れないがそれを

7÷2=3 余り 1

と書いて3を商、1を余りという。これは

\[ 7=3×2+1 \\ 7/2=(3×2+1)/2=3×2/2+1/2=3+1/2 \]

と書いても同じである。特に最後の式は、\(3\frac{1}{2}\) と書いてサンカニブンノイチ、あるいはサンとニブンノイチと読み帯分数と言う。 \(\frac{7}{2}\) の様に分子が分母より大きい時、これを仮分数、小さい時を真分数と言うこともある。(分母と分子が等しい時は整数である｡) また、\( \frac{14}{4}=\frac{7\cdot 2}{2\cdot 2}=\frac{7}{2}\) であるが 14と4は共に2で割れるので、分母と分子の2が打ち消しあってより簡単な \(\frac{7}{2}\) という分数になる。この操作を約分と言い、今の場合の7と2の様にこれ以上約分出来ない分母と分子を互いに素であると言う。

割る数を \(q ∈ \boldsymbol{N}\) とすると、余りは \(0, 1, 2, ..., q-1\) のどれかである。余りが 0 の時が割り切れる場合である。

今まで正の分数だけ扱って来たが、分数にも負の数を考えることが出来る。 \(-1\) の逆数は \(-1\) なので、分母と分子が共に正か負なら分数は正、どちらかが負で他方が正なら分数は負である。

自然数 (一般には整数) を2で割った余りは必ず 0 か 1 であるが、0 (つまり、割り切れる) の時の整数を偶数 (Even numbers)、1 (割り切れない) の時の整数を奇数 (Odd numbers) という。集合記号では、これらを

\[ E=\{..., -4, -2, 0, 2, 4, ...\} ,\quad O=\{..., -3, -1, 1, 3, ...\} \]

と表わす。明かに \(E\) と \(O\) に共通部分は無く

\[ E \cap O = ∅ ,\quad E \cup O = E + O = \boldsymbol{Z} \]

である。同様に 3 で割った時も、余りは 0 か 1 か 2 のどれかなので、 \(N_0=\{..., -3, 0, 3, ...\}\)、\(N_1=\{..., -2, 1, 4, ...\}\)、\(N_2=\{..., -1, 2, 5, ...\}\) として

\[ N_0 \cup N_1 \cup N_2 = N_0 + N_1 +N_2 = \boldsymbol{Z} \]

である。多少難しい言葉では、これを整数 \(\boldsymbol{Z}\) の類別と言い、また \(n ∈ N_2\) の時 \(n ≡ 2 (\hbox{mod} 3)\) と書いてこれを module 3 の合同式と言う。

素数、素因数分解、ベキ乗、最大公約数、最小公倍数、分数の約分、通分

2以上の自然数で1とそれ自身以外では割り切れない自然数を素数と言う。 20までの素数を具体的に書くと

素数={2 ,3, 5, 7, 11, 13, 17, 19, ...}

である。これを求めるには、まず4以上の偶数は必ず2で割り切れるので除いておいて、3 以上の奇数を並べておき、3 以外の 3 の倍数を全て取り去る。次に、5 の倍数を除き、7 の倍数を除き、... としていくと、結局素数だけが残る。この様にして素数を求める方法を、エラトステネスの篩(ふるい)と言う。エラトステネスは古代ギリシャの数学者である。

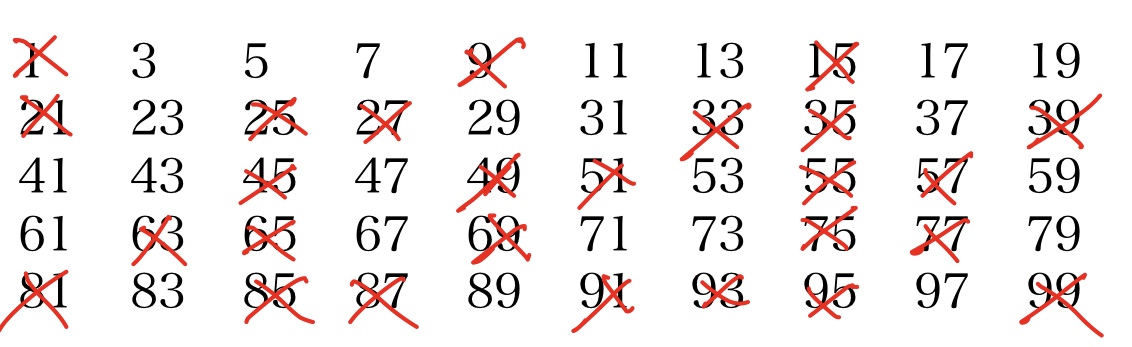
図5: エラトステネスの篩(ふるい)

ここから、100 までの素数は、 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 であることが分かる。

任意の自然数は常に一意的に素数の積で表される。例えば18 は2 で割れるが、その商の9はさらに3で割れるので 18 =2×3×3 と分解される。136 は 136=2×68=2×(2×34)=2×2×34=2×2×(2×17)=2×2×2×17 である。今の場合のように、同じ素数が繰り返し現れる場合には、ある数のベキ乗(累乗とも言う)の書き方を使って

2×2×2=2³

3×3=3²

等と書くと便利である。2 を3回掛けることを2³と書き2の3乗、3 を2回掛けることを3²と書き 3の2乗(あるいは自乗)と言う。 2乗、3乗はまた平方、立方とも言う。自然数の右肩に乗っている小さい数をベキ(冪)とか指数とか言う。ある数の1乗はその数自身、またある数の0乗は常に1であると約束する。(0の0乗は考えない。) また、掛け算記号×はしばしば・(中点)で表わされる。 (また、数式では誤解が起こらない限り \(xy\) の様に中点すら省略する場合もある。) 上の例では

18=2・3²

136=2³・17

である。一般に \(n ∈ \boldsymbol{N}\) を任意の自然数とすると、 \(n_1, n_2, n_3, ... \) を 0 か自然数のいずれかとして素数のベキ乗を用いて

\[ n=2^{n_1} \cdot 3^{n_2} \cdot 5^{n_3} \cdot 7^{n_4} \cdot ... \]

と表わされる。(\(n\) の下付きの添字は、自然数の値を区別するために用いられる。) これを自然数の素因数分解と言い、ここに現れる0以外の \(n_1, n_2, n_3, n_4, ... \) をもつ素数を素因数と言う。

ある自然数が(それと同じか)それより小さい自然数で割りきれる時、小さいほうの自然数を大きい方の自然数の約数、大きい方の自然数を小さい方の自然数の倍数という。例えば、6は12の約数、12は6の倍数である。また、2つの自然数がある時、それらの共通する最大の約数を最大公約数、共通する最小の倍数を最小公倍数という。12と6の例では、最大公約数は6、最小公倍数は12である。

最大公約数、最小公倍数を見つけるには、二つの自然数のそれぞれを素因数分解して、そこに現れる素数の個数を数えればよい。すなわち、それらに共通に現われる素因数のもつ相等しいか小さい方のベキ乗を取って、それらを全て掛け合わせれば最大公約数が、どちらかに現れる素因数の相等しいか大きい方のベキ乗をとって、それらを全て掛け合わせれば最小公倍数が得られる。最大公約数と最小公倍数を掛け合わせると元の2つの自然数を掛けたものに一致する。 18と136の例では、最大公約数は 2¹=2、最小公倍数は 2³・3²・17=136・9=1224 であり、 2つかけたものは 2⁴・3²・17=2・1224=2448 である。 2つの自然数 (例えば分数の分母と分子) が互いに素なのは、それらの最大公約数が1の場合である。この場合は最小公倍数は2つの自然数の積に一致する。

最大公約数と最小公倍数は、分数の約分や通分に絶対に必要である。例えば、18/136 は分子と分母に含まれる最大公約数 2で割る事により 18/136=(2・9)/(2・68)=9/68 となって、より簡単な分数になる。 9 と 68 は互いに素であり、これ以上簡単な分数にはならない。また、1/18+1/136 の計算では、2 つの分数の分母を最小公倍数の1224 に揃える事により、1/18+1/136=4・17/1224+9/1224=(68+9)/1224=77/1224 と計算される。77の素因数分解は77=7・11より、これ以上簡単にはならない。つまり、77と1224は互いに素である。分数の計算では、あらゆる段階で約分をして最も簡単な表わし方にしておくと計算が楽になる。

素数については、今だよく分かってない事が多い。例えば、素数が無限個あることは古代ギリシャの時代から既に分かっているが、{3, 5}, {5, 7}, {11, 13} の様に2だけ違う素数(双子素数という)が無限個あるかどうかは今だに分かっていない。また、4より大きい偶数は必ずニつの素数の和で表わされる (例えば、138=41+97) ということももっともらしいが、まだ証明されていない。こういう事を扱う分野は数論と言って、数学の大変難しい一分野である。

分数と小数の関係、循環小数

分数は位取りの考え方を用いて、ある種の少数と完全に同値である。 0から9までの自然数を1の位(くらい)として、すべての数をこれらだけで表わす表記法を十進法といい、これらの数字を十進数と言う。10の位を1の位の数に0をつけて表わし、 1の位の数を添えて、二桁の数字を表わす。例えば、32=3×10+2×1である。同様に三桁の数字は、例えば869=8×100+6×10+9×1である。ここに現れる10, 100, ... は10を何回か掛けたものであり、以前出てきた10 のベキ乗の表記法を用いて

...

1000=10×10×10=10³

100=10×10=10²

10=10¹

と表わされる。10 のベキがひとつずつ減るごとに10分の1小さくなっていくので、小さい方の位取りも

1=10⁰

1/10=10^-1

1/100=10^-2

1/1000=10^-3

...

と表わされる。1/10を単位(物の量を測る時の基準となる一塊りの量)とする数を下(しも)一桁の小数と言って、自然数.nで表わす。ここに、n は0, 1, ...,9 のどれかである。下二桁、下三桁、... の小数も同様である。数字の間の下点、ピリオド(少なくとも、日本では)を小数点と言う。例えば、下三桁の小数 2106.305 は

2106.305=2×10³+1×10 ²+0×10¹+6×10⁰+3×10^-1 +0×10^-2+5×10^-3

のことを示す。

1=10×(1/10) を用いて、分数は全て小数で表わすことが出来る。例えば、

1/5=10×(1/10)/5=10/5×(1/10)=2×10^-1=0.2

である。10は2と5で割れるから、分母が素因数2と5しか含まない自然数からなる分数は必ず有限の桁数の小数で表わされる。また、たとえ分母に素数があっても、もし分子に同じ素数が有ればこれらは約分出来る。この様な分数を、割り切れる分数とか有限小数とか言う。しかし、分数は常に割り切れるわけではない。例えば、1/3 は10を3で割ると常に1だけ余りが出るから

1/3=10×(1/10)/3=10/3×(1/10)=(3×3+1)/3×(1/10)=(3+1/3)×(1/10) =3×(1/10)+1/3×(1/10)=0.3+1/3×(1/10)

この二項目の1/3に、再び上の式を入れると

1/3=0.3+(0.3+1/3×(1/10))×(1/10)=0.3+0.3×(1/10)+1/3×(1/100) =0.3+0.03+1/3×(1/100)=0.33+1/3×(1/100)

この操作を続けて行くと

1/3=0.333+1/3×(1/1000)=0.3333+1/3×(1/10000)= ...

と永遠に続く。つまり3が繰り返して現れて、有限個の数字では決して表わしきれない。これを、\(1/3=0.333 ... =0.\dot{3}\) と書いて循環小数といい、無限に繰り返す3をその上の点 (dot)で表わす。もう一つの例として、134/111 を考えてみる。まず、134/111=1+23/111 次に230を111で割ると2が立って8余るから、今度は800を111で割って7が立ち23余る。23が再び現れてきたので、後はこれらの繰り返しである。そこで、\(134/111=1.207207207 ... =1.\dot{2}0\dot{7}\) となる。この事は、電卓を使っても確かめられる。dotで挟まれた 207 を循環節と言う。 111 で割った時の余りは、0, 1, 2, ...,110 までの自然数のどれかだから、有限回の割り算を行ううちに必ず同じ余りが現れることになる。まとめると、分数は必ず割り切れる小数か循環小数で表わされる。

(追記) 1/3=0.333 ... という書き方は不思議に思えるかもしれない。この両辺を3倍すると 1=0.999 ... つまり、0.999 ... は 1 と考えるのである。

無理数、超越数、実数、数直線

無限に伸びる直線のどこか一点(原点という)に0を取り、長さ1の単位を決めて、原点からの距離により数を直線上の点に対応させたものを数直線 (number line) というが、数直線には分数に対応する小数の点(有理点という)以外にも、非常に多くの無限小数に対応する点が含まれていることが知られている。循環しない無限小数としては、\(\sqrt{2}=1.414213 ... \) 等の無理数や \(π =3.141592 ... \) 等の超越数がある。

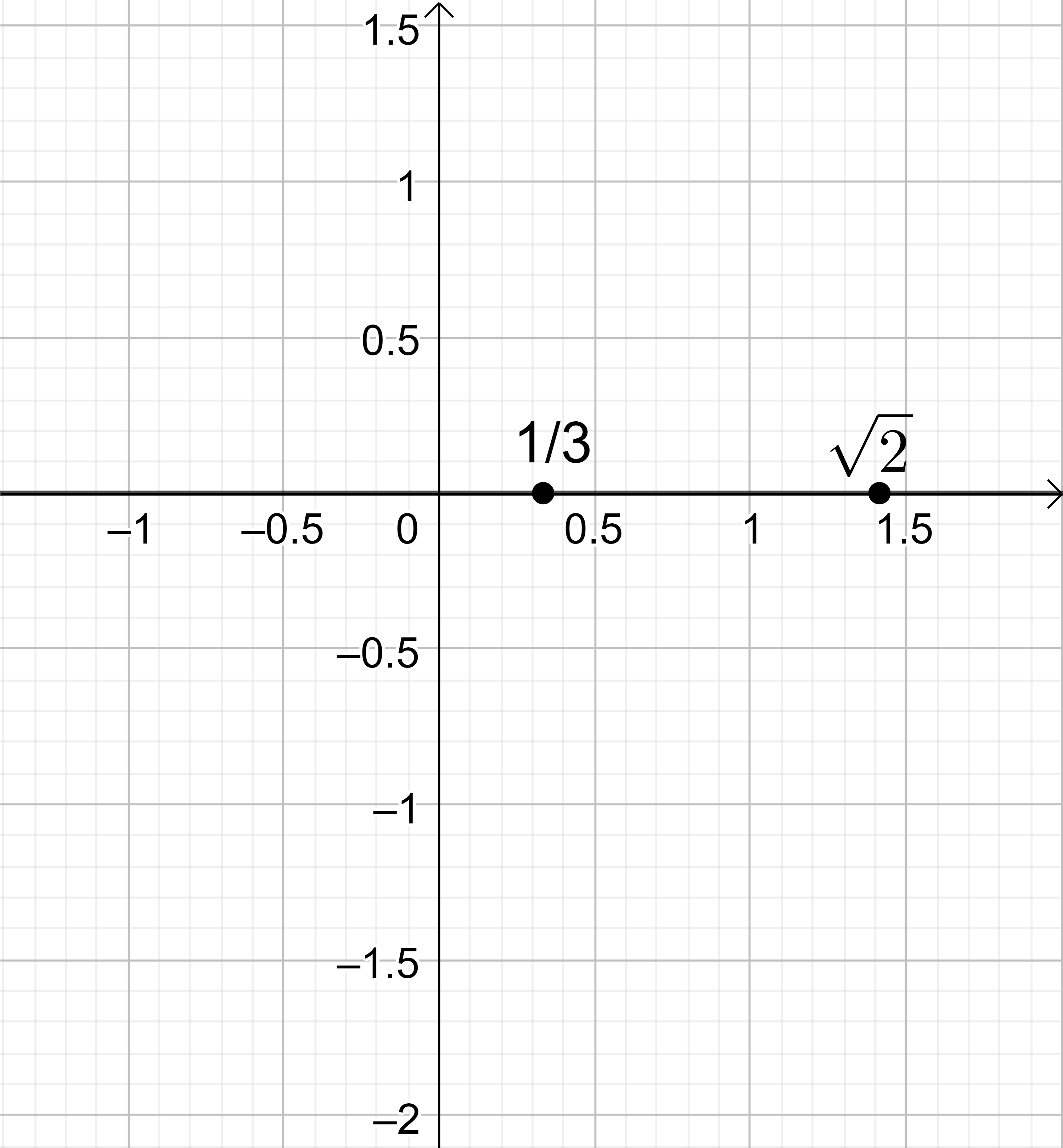
図6: 数直線上の \(\frac{1}{3}\) と \(\sqrt{2}\)

\(\sqrt{2}\) は、ピタゴラスの定理から知られる様に一辺1の正方形の対角線の長さであるが、それは二回掛ければ2となる様な数で2の平方根と言われる。これが整数/整数のかたちの分数で表わされない事は、高校1年の後期に学ぶ背理法を用いて簡単に証明される。

いま事実と反して、\(\sqrt{2}\) が互いに素な二つの自然数 \(p, q\) によって \(\sqrt{2}=p/q\)と表されたと仮定しよう。(最大に約分することによって、 \(p\) と \(q\) の最大公約数はあらかじめ 1 にしてあるとする。)この式を2乗することによって、\( p^2=2×q^2\) が得られる。\(p, q\) は自然数だから、 \(p\) は偶数でなければならない。(もし \(p\) が奇数なら \(p^2\) は奇数になる！) そこで、\(p\) はある自然数 \(k\) を用いて \(p=2k\) と表わされる。これを \(p^2=2×q^2\) に代入して、\(4×k^2=2×q^2\) つまり \(q^2=2×k^2\) が得られる。再び \(q\) は偶数だから、\(p\) と \(q\) が共に偶数となって、互いに素であるというはじめの仮定に矛盾する。したがって、\(\sqrt{2}=p/q\) と表わされるというはじめの仮定が間違っていて、\(\sqrt{2}\) は分数では表わされないことになる。

(練習問題-1) \(n\) を 3 より大きい素数として、\(\sqrt{n}\) は無理数であることを、上と同様にして示せ。

(練習問題-2) \(\sqrt{4}=2\) であるが、\(\sqrt{4}\) が無理数である事は、当然のことながら上の様にしては導けない。何故か？

\(\sqrt{2}\) は数直線上の点で、

\[ 1.4 < \sqrt{2} < 1.5 \\ 1.41 < \sqrt{2} < 1.42 \\ 1.414 < \sqrt{2} < 1.415 \\ 1.4142 < \sqrt{2} < 1.4143 \\ ... \]

と間隔を狭めていった極限として求めることが出来る。この様に、相異なる二つの有理数の間には、その間隔がいかに小さくても無限の数の無理数が存在する。

有理数と無理数を合わせて実数 (Real numbers) といって集合記号 \(\boldsymbol{R}\)で表わす。つまり、無理数は有理数以外の実数であって {無理数}= \(\boldsymbol{R} \backslash \boldsymbol{Q}\) である。実は実数と数直線を対応させることには無理があって、より厳密な実数の定義には数直線などという視覚には依存しない議論が必要である。その様な理論は、1870年代にドイツの数学者デデキントによる与えられた。デデキント切断は、有理数全体の切断により実数を定義する方法である。これにより、数列の極限や実数の連続性という非常に重要な性質が明らかになるが、それは既に高校生のレベルを越えている。また、超越数も無理数の一種であるが、それについてもここではこれ以上立ち入らないことにする。

数学用語として数(すう)と言えば、それは一般には実数(あるいは、それを拡張した複素数)のことを指す。そこでは、有理数の時と同様、加減乗除(四則)の演算(計算)が(0で割ることを除いては)自由に出来る。実は、有理数から出発して計算のルールが成り立つように数の概念を拡張していくと必然的に実数と複素数の概念に到着するのである。加減乗除が自由に出来る数の集合のことを体(field)という。有理数体: \(\boldsymbol{Q}\)、実数体: \(\boldsymbol{R}\)、複素数体: \(\boldsymbol{C}\)、等々 ... 。数の集合としては

\[ \boldsymbol{N} ⊂ \boldsymbol{Z} ⊂ \boldsymbol{Q} ⊂ \boldsymbol{R} ⊂ \boldsymbol{C} \]

の関係がある。

表: 数の体系 (分類)

\[ \begin{array}{l} 数 (複素数) \left\{ \begin{array}{l} 実数 \left\{ \begin{array}{l} 有理数 \left\{ \begin{array}{l} 整数 \left\{ \begin{array}{l} 正 (自然数)(1, 2, \cdots) \\ 0 \\ 負 (-1, -2, \cdots) \\ \end{array} \right. \\ 分数 \left\{ \begin{array}{l} 正 ({1 \over 2}, {1\over 3}, \cdots) \\ 負 (-{1 \over 2}, -{1\over 3}, \cdots) \\ \end{array} \right.\\ \end{array} \right. \\ 無理数 \left\{ \begin{array}{l} 正 (\sqrt{10}, \cdots) \\ 負 (-\sqrt{10}, \cdots) \\ \end{array} \right. \\ \end{array} \right. \\ 虚数 (i, 1+i, {1-i \over \sqrt{2}}, \cdots) \\ \end{array} \right. \end{array} \]

指数法則と対数、ネピア数、自然対数の底

素因数分解と十進数のところで既に説明したように、ベキ乗の概念を用いると非常に大きな数や小さい数を簡単に表すことができる。 10のベキ乗を例に取ると、それらには「指数法則」と呼ばれる次の計算のルールが存在する。

\[ 10^n ×10^m = 10^{(n+m)} \\ (10^n)^m = 10^{(n×m)} \]

上の関係式を「和の指数法則」、下の関係式を「積の指数法則」という。 (一般には、\((10^n)^m \neq 10^{(n^m)}\) であるので、\(10^{n^m}\)という書き方は避ける。) ベキ乗はカッコの場合と同様、掛け算、割り算よりも先に計算する。和の関係式は、\(10^n\) が 10 を n 回掛ける意味であることから明らかである。積の関係式は、\( (10^n)^m=10^n × 10^n × ... × 10^n\) と \(10^n\) を m 回掛けることから、和の関係式を繰り返し使うことによって証明出来る。「和の指数法則」は、二つの数の掛け算は、指数で表わしておくと指数の和に、「積の指数法則」は、ベキ乗のベキ乗は指数の掛け算に帰着されることを示している。

「指数法則」を用いると、特別な場合のベキ乗の値を求めることが出来る。例えば、「和の指数法則」で \(m=0\) とおくと \(10^n × 10^0=10^n\) で \(10^n\) は決して0にならないので、これで両辺を割ると \(10^0=1\) であることが分かる。また、\(10^n × 10^{(-n)}=10^{(n-n)}=10^0=1\) より、\(10^{(-n)}\) は \(10^n\) の逆数、つまり \(10^{(-n)}=1/{10^n}\) であることが分かる。

上では、指数法則を用いて \(n、m\) を自然数から整数にまで拡張したが、 \(n、m\) は更に有理数や実数、更には複素数にまで拡張できる。例えば、 \(10^{\frac{1}{2}}\) は「積の指数法則」を用いて

\[ (10^{\frac{1}{2}})^2=10^{\frac{1}{2} × 2}=10^1=10 \]

より、二回掛ければ10となる数 \(\sqrt{10}\)である。\(\sqrt{10} > 0\) という規約なので、二回掛ければ10となる数は \(\pm \sqrt{10}\)であるが、全ての実数 x について \(10^x > 0\) と約束するので、\(10^{\frac{1}{2}}=\sqrt{10} > 0\) である。同様に、\(10^{\frac{1}{n}}=\sqrt[n]{10}\) は 10 の \(n\)-乗根であり、また \(p ∈ \boldsymbol{Z}\) を任意の整数、\(q\) を正の整数として

\[ (\sqrt[q]{10})^p=(10^{\frac{1}{q}})^p=10^{\frac{p}{q}}=(10^p)^{\frac{1}{q}} =\sqrt[q]{10^p} \]

が成り立つ。

上で分数指数のベキ乗は累乗根であることが分かったが、無理数のベキ乗の場合にも、その答えを実数の中に見出すことが出来る。例えば、\(10^{\sqrt{2}}\) は電卓を使って計算すると

10¹=10

10^1.4=25.11864 ...

10^1.41=25.7039 ...

10^1.414=25.9417 ...

10^1.4142=25.9537 ...

10^1.41421=25.9543 ...

10^1.414213=25.9545 ...

...

\(10^{\sqrt{2}}\)=25.95455351947 ...

となる。一般に数の列を数列、上の様に前の数字より後ろの数字が必ずより大きくなっている数列を単調増大列という。 \(10^{\sqrt{2}} < 10^{1.5} < 10^2=100\) の時の様に、全ての数がある一定の数より小さい時、その様な数列を単調(増大)有界列という。デデキント切断により実数を定義すると、単調有界列は必らず収束するという大変明快な定理を証明する事が出来る。これを実数の連続性という。この命題は、数の概念を実数まで広げておけば、一つの単調有界列の極限を必らず一つの実数に見つけることが出来るということを保証している。

結局、全ての実数 \(x, y ∈ \boldsymbol{R}\) に対して、指数法則

\[10^x \cdot 10^y=10^{(x+y)} \quad , \quad (10^x)^y=10^{(xy)} \]

が成り立つ。

これまで、10 のベキ乗について指数法則を説明して来たが、実際には任意の正の実数 \(a ∈ \boldsymbol{R}\), \(a > 0\) のベキ乗について指数法則が成り立つ。(\(a=1\) の時は、任意の数 \(x\) に対して \(1^x=1\) である。) つまり、

\[a^x \cdot a^y=a^{(x+y)} \quad , \quad (a^x)^y=a^{(xy)} \]

(注意: \( 0^0\) は考えない。)

(練習問題) 積の指数法則を複数回用いることにより、 \(\left(\sqrt{2}^{\sqrt{2}}\right)^{\sqrt{2}}=2\) であることを示せ。これは、電卓を使っても確かめられる。

実数 \(x, y\) に対して \(y=10^x\) の時 \(x=\log y\) (より正確には \(x=\log_{10} y\) と書いて \(x\) を \(y\) の対数 (より正確には常用対数)という。(ベキ指数の実数の場合への一般化である。) また、10 を常用対数の底という。常用対数に対しては特に \(x=\hbox{Log}\ y\) と書くこともある。 \(y\) を \(x\) の関数と見て \(x=-\infty\) から \(\infty\) に変化する時、\(10^0=1\) であり\(x > 0\) のところでは \(y\) は 1 から急速に増大し、\(x < 0\) のところでは \(x\) が \(-\infty\) に近づくにつれ 0 に向かって急速に減少する。対数の底 10が \(a > 1\) の時にも、上と同様のことが成り立つ。この場合は、 \(y=a^x\)、\(x=\log_a y\) と書く。 \(0 < a < 1\) の場合にも、指数関数 \(y=a^x\)、対数関数 \(x=\log_a y\) を定義できるが、この場合は \(y=a^x=(1/a)^{(-x)}\) より、指数関数のグラフは \(a > 1\) の場合と比べて \(x\)-軸の正の方向と負の方向が逆になる。\(a > 1\) の特別の場合として、ネピア数 (自然対数の底ともいう) \(e=2.71828 ... \) を用いた指数関数 \(y=e^x\)や対数関数 \(x=\log_e y\) もよく用いられる。特にこの場合を自然対数 (natural logarithm) といい、\(e\) を省略して \(x=\log y\) と書いたり、\(x=\ln y\) と書いたりする。普通、指数関数、対数関数といえばこの場合をさす。特別の場合として、\(\log e=1, \log 1=0\) である。これらは、 \(e^1=e, e^0=1\) に対応する。

図7: 指数関数 \(y=a^x\) のグラフ (\(a=10, e, 1, 0.5\))

図8: 指数関数 \(y=e^x\) と対数関数 \(y=\log x\) のグラフ

指数関数と対数関数は、互いに逆関数である。また、指数法則といえば普通

\[ e^x \cdot e^y=e^{(x+y)} \quad , \quad (e^x)^y=e^{(xy)} \\ \log ab = \log a + \log b \quad , \quad \log a^y=y \log a \]

をさす。ここに、\(x, y\) は任意の実数、\(a , b > 0\) は任意の正の実数である。

(練習問題) 上の二行目の「対数法則」を証明せよ。

(略解) \( a=e^x \ , \ b=e^y \) として、指数法則より \( ab=e^x e^y=e^{(x+y)} \)。そこで \( x+y=\log ab \)。ここで、\(x=\log a, y=\log b\) を用いると

\[ \log a + \log b = \log ab \]

また、\( a^y=(e^x)^y=e^{(xy)} \) より \(xy=\log a^y \)。 \( x=\log a\) を用いると

\[ \log a^y=y \log a \]

(追記) 自然対数の底 \(e\) に対して、指数関数 \(a=e^x\) の逆関数である自然対数 \(\log\) を \(x=\log a\) で定義すると、\(x\) を代入して

\[ a=e^{\log a} \tag{1} \]

が任意の正の実数 \(a > 0\) に対して成り立つ。同様に \(a\) を消去して

\[ x=\log e^x \tag{2} \]

が常に成り立つ。これらは、展開公式や指数法則などと同様 \(a\) や \(x\) が何であっても成り立つ「恒等式」である。そこで、(1) で \(a\) を \(b\) に変えたり \(ab\) に変えたりして

\[ b=e^{\log b} \\ ab=e^{\log ab} \]

が得られる。一方、指数法則から

\[ ab=e^{\log a} e^{\log b}=e^{(\log a + \log b)} \]

であるので、両辺の \(\log\) を取って (2) を使うと

\[ \log ab = \log e^{(\log a + \log b)} = \log a + \log b\]

となる。ここに、\(a, b > 0\) である。

同様に、(1) を \(y\)-乗して指数法則 \(e^{(xy)}=(e^x)^y\) with \(x=\log a\) を使うと

\[ a^y=(e^{\log a})^y=e^{y \log a} \]

そこで、\(\log\) を取って (2) を使うと

\[ \log a^y = \log e^{y \log a} = y \log a \]

ここに、再び \(a > 0\) である。

(1) を使えば、任意の対数の底 \(a > 0\) の指数法則、対数法則を自然対数の底のそれらに帰着させることができる。すなわち、(1) の \(x\)-乗を取って、それを \(y\) と置くと指数法則から

\[ y = a^x = e^{x \log a} \]

ここで、 \(a \neq 1\) として、底 \(a\) の \(\log\) を取ると \(x=\log_a y\)。一方、底 \(e\) の \(\log\) (自然対数) を取ると \(\log y = x \log a\)。そこで、\(x\) を比較して \[ \log_a y = (\log y)/(\log a) \]

特に \(y=e\) の時、\(\log e = 1\) より \(\log_a e = 1/(\log e)\) である。また \(y=b > 0, b \neq 1\) とすると、\(\log _a b = (\log b)/(\log a)\) より

\[ (\log_a b)(\log_b a)=1 \quad \hbox{for} \quad a, b > 0 \ \hbox{and} \ a, b \neq 1 \]

まとめると、一般に

\[ a^x = e^{x \log a} \quad , \quad \log_a x = \frac{\log x}{\log a} \tag{3} \]

つまり、指数関数で \(a\) を \(e\) に変えると \(x → x \log a\) に、底が \(a\) の対数関数を \(e\) に変えると全体を \(\log a\) で割ればよい、という簡単なルールが存在する。

(3) を使うと、一般の \(a > 0\) を底とする指数法則や対数法則を簡単に導くことができる。まず、\(e^x e^y=e^{(x+y)}\) で \(x→x \log a, y→y \log a\) と変えて

\[ e^{x \log a} e^{y \log a} = e^{(x \log a + y \log a)} = e^{(x+y) \log a} \]

そこで

\[ a^x a^y = a^{(x+y)} \]

また、\((e^x)^y=e^{(xy)}\) で \(x → x \log a\) と変えて

\[ (a^x)^y = (e^{(x \log a)})^y = e^{(xy \log a)} = (e^{\log a})^{(xy)} = a^{(xy)} \]

次に、対数法則は

\[ \log_a xy = (\log xy)/(\log a) = (\log x + \log y)/(\log a) \\ = (\log x)/(\log a) + (\log y)/(\log a) = \log_a x + \log_a y \\ \log_a b^x = (\log b^x)/(\log a) =(x \log b)/(\log a) \\ = x (\log b)/(\log a) = x \log_a b \]

ここに、\(x, y\) は任意の実数、\(a, b > 0\) は任意の正の整数である。また、対数の底は \(a \neq 1\) だけ考えるものとする。

ここまで \(x, y\) や \(b\) は実数と仮定してきたが、実は更に進んだ Riemann 面という考え方を用いると、これらを複素数 \(z\) にまで拡張することができる。すなわち \(a^z\) を \( a^z = e^{z \log a}\) と考えるのである。更に複素積分による表示を用いると \(z \ne 0\) に対して \(\log z\) も矛盾なく定義することができる。これらについては、「代数」、「解析」の項を参照して頂きたい。

(追記の項、終わり)

\(e\) は \(π\) と同様に超越数であり次の様にして求められる。

(1+1)¹=2

(1+1/2) ²=1.5²=2.25

(1+1/3) ³=1.333 ...³=2.370370370 ...

(1+1/4)⁴=1.25⁴=2.44140625

(1+1/5)⁵=1.2⁵=2.48832

(1+1/6)⁶=2.521626371746 ...

これは、有理数の単調増大列であり、かつ有界であることを証明することが出来る。 (証明は多少面倒なので省略する。) そこで、実数の連続性からその極限の実数が存在する。それが \(e\) である。これを

\[ e = \lim_{n→\infty} \left(1+\frac{1}{n}\right)^n = 2.71828 18284 59045 ... \]

と書く。また別の定義は

\[ e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+ ... \]

とも表わすことが出来る。ここに、自然数 \(n\) に対して \(n!= 1・2・3・...・n\) は 1 から \(n\) までの自然数を全て掛けたものであり、 \(n\) の階乗 (factorial) という。

(練習問題) 二項定理を用いて、上の二つの \(e\) の定義が同等であることを証明せよ。

複素数

全ての実数 \(x\) は、二乗すると 0 か正である。しかし、高度な数学では、二乗したら負となる数「虚数単位」\(i\) を導入して、実数を複素数 (Complex numbers) にまで広げることで、美しく豊かな数学の世界が広がっている事が分かっている。ここでは高校数学の範囲内で、簡単な複素数の基本的事項を学ぶ。

\(i^2=-1\) として二つの実数の組み (\(x, y\)) に対して \(z=x+yi\) (あるいは、\(z=x+iy\)) とおき、これを複素数という。 \(x\) と \(y\) を、複素数 \(z\) の実部と虚部という。\(x=0\) の時、\(yi\) を純虚数という。虚部の符号を変えたものをもとの複素数の複素共役といい、 \(z^* =x-yi\) あるいは \(\overline{z}=x-yi\) で表わす。複素数を表わす文字としては、\(z\) 以外にギリシャ文字の α β とか ω もよく使われる。複素数の足し算、掛け算は、 \(a , b, c , d\) を任意の実数として、

\[ (a+bi)+(c+di)=(a+c)+(b+d)i \\ (a+bi)(c+di)=(ac-bd)+(ad+bc)i \]

である。つまり、\(i^2=-1\) の約束のもとに、これまでの計算のルールが常に成り立つとして計算する。同様に複素数のベキ乗についても

\[ z^n z^m=z^{n+m} \quad , \quad (z^n)^m=z^{nm} \]

等が成り立つ。

\(z=x+yi\) の時、\(zz^*=(x+yi)(x-yi)=x^2+y^2\) より、複素数 \(z\) の絶対値を

\[ |z|=\sqrt{zz^*}=\sqrt{x^2+y^2} \]

で定義する。z の逆数は

\[ \frac{1}{z}=\frac{z^*}{(zz*)}=\frac{(x-yi)}{x^2+y^2}\]

であるので、複素数の分数は

\[ \frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{c^2+d^2}=\frac{ac+bd}{c^2+d^2}+\frac{bc-ad}{c^2+d^2}i \]

と計算される。この計算は、無理数の分数の有理化に類似している。

複素数には、複素平面での極座標表示や三角関数への応用等、多くの美しく有用な性質があるが、それらについてはまた別の項目に譲ることにする。

(参考文献)

1. 「零の発見: 数学の生い立ち」吉田洋一著、岩波新書

2. 「One, two, three ... Infinity: Facts and Speculations of Science」George Gamow, Dover Books on Mathematics

3. 「数学入門(上、下)」遠山啓著、岩波新書

4. 「解析概論」高木貞治著、岩波書店

(「数について」の項、終わり)

自然数、整数、有理数、実数、複素数